【机器学习】 一些入门AI的基础知识整理

概念基础

监督学习/无监督学习

监督学习

是指从带有标签（Label）的训练数据中学习模型，然后对新的无标签数据进行预测。模型通过学习输入特征（X）与输出标签（Y）之间的映射关系，建立预测函数$y=f(x)$。目标是最小化预测值和真实值之间的误差，可以通过准确率、召回率、MSE等指标量化模型性能。

任务类型	输出形式	典型算法	应用场景
分类	离散类别	逻辑回归、SVM、决策树、随机森林	垃圾邮件识别、图像分类、疾病诊断
回归	连续数值	线性回归、岭回归、XGBoost	房价预测、销量预测、股票分析

• 适用场景：充足标注数据、预测目标明确、可解释性要求高（需要解释决策的任务诸如金融风控）

• 优缺点：预测精度高、可解释性强（尤其线性模型）；依赖标注数据（获取成本高）、对未知分布泛化能力有限。

无监督学习

无监督学习从无标签数据中挖掘隐藏模式或结构，不提供明确的正确答案，模型自主发现数据内在规律。无需标注，目标可能是聚类、降维或者关联分析。

任务类型	目标	典型算法	应用场景
聚类	数据分组	K-means、DBSCAN、层次聚类	用户分群、异常检测、推荐系统
降维	减少特征维度	PCA、t-SNE、Autoencoder	数据可视化、特征压缩、去噪
关联规则	发现数据项间关系	Apriori、FP-Groth	购物篮分析
生成模型	学习数据分布生成样本	GAN、VAE	图像生成、数据增强

• 适用场景：探索性数据分析、数据预处理（降维后供监督模型）、异常检测（聚类发现离群点）、数据生成（小样本生成）

• 优缺点：无需标注数据，可发现隐藏模式；难以量化评估

评估指标

对于分类问题：

混淆矩阵

	预测为正	预测为负
真实为正	True Positive（TP）	False Negative（FN）
真实为负	False Positive（FP）	True Negative（TN）

准确率（Accuracy）

$$
Accuracy = \frac{TP + TN}{TP + TN + FP + FN}
$$

所有预测正确的样本占比，但在类别不平衡时失效

精确率（Precision）

$$
\text{Precision} = \frac{TP}{TP + FP}
$$

预测为正的样本中实际为正的比例，关注”预测的准不准”，注重减少误报（如垃圾邮件分类中，避免将正常邮件判为垃圾）

召回率（Recall）

$$
\text{Recall} = \frac{TP}{TP + FN}
$$

真实为正的样本中被正确预测的比例，关注”找的全不全”，注重减少漏检（如癌症筛查、缺陷检测）

F1-Score

$$
F_1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}
$$

Precision和Recall的调和平均数，平衡精确率和召回率，适用于类别不平衡场景

假正率（FPR）

$$
\text{FPR} = \frac{FP}{FP + TN}
$$

真正率（TPR=Recall）

$$
\text{TPR} = \frac{TP}{TP + FN}
$$

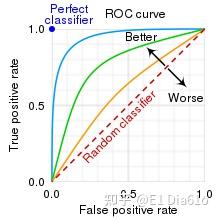
ROC曲线（Receiver Operating Characteristic）

横轴为假正率，纵轴为真正率。调整分类阈值（如逻辑回归的0.5阈值），计算不同阈值下的（FPR, TPR）点连线

• 左上角(0,1)：完美分类器

• 对角线：随机猜测

• 曲线越靠近左上角，模型越好

AUC(Area Under Curve)

ROC曲线下的面积

• 取值范围：0.5（随机）~1（完美）

• 物理意义：模型将正样本排在负样本前面的概率

• 优点：

  • 不受类别分布影响

  • 不受阈值影响（评估整体性能）

对于回归问题

均方误差MSE（Mean Squared Error）

$$
MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2
$$

• $y_i$：第 $i$ 个样本的真实值
• $\hat{y_i}$：第 $i$ 个样本的预测值
• $n$：样本数量

特点

1. 放大大误差：平方项使较大误差对结果影响更显著

2. 单位问题：与原始数据单位平方一致（如房价预测结果为”万元²”）

3. 可导性：光滑可导，适合梯度下降优化

应用场景

• 模型训练时的损失函数（如线性回归）

• 需要惩罚显著偏离的预测（如金融风险预测）

均方根误差RMSE （Root Mean Squared Error）

$$
RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2}
$$

特点

1. 恢复单位：与原始数据单位一致（如”万元”）

2. 可比性：与MAE相比更重视大误差（因平方根弱化了MSE的放大效应）

3. 对异常值敏感：仍受极端值影响

   应用场景

• 业务结果汇报（单位直观）

• 需要平衡普通误差与大误差的评估（如房价预测

平均绝对误差MAE （Mean Absolute Error）

$$
MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y_i}|
$$

特点

1. 线性惩罚：所有误差等权重处理

2. 鲁棒性：对异常值不敏感

3. 不可导：在零点不可导，不适合直接用于梯度下降

应用场景

• 异常值较多的数据（如传感器数据清洗）

• 需要直观理解平均误差大小的场景（如库存需求预测）

R²分数（R-Squared，决定系数）

$$
R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y_i})^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}
$$

• yˉ​：真实值的均值

  解读

• 分子：模型预测的误差（MSE）

• 分母：基准模型（总是预测均值）的误差

• 取值范围：

  • R2=1：完美预测

  • R2=0：等同于均值预测

  • R2<0：模型比均值预测更差

特点

1. 无量纲：不受数据单位影响

2. 可比性：可用于不同数据集间的模型比较

3. 易误解：高R²不一定代表模型好（可能数据本身易预测）

指标	敏感度	单位	优化适用性	业务解释难度
MSE	高（平方放大）	原单位²	★★★★★（可导）	较难（单位平方）
RMSE	中	原单位	★★★★☆	较易
MAE	低（线性）	原单位	★★☆☆☆（不可导）	最易
R²	相对性	无	-	需统计背景

对于聚类问题

轮廓系数（Silhouette Coefficient）

1. 核心思想

衡量一个样本在聚类中的紧密性和分离性，即：

• 同簇样本是否足够接近

• 不同簇样本是否足够远离

2.计算公式

对于单个样本i

$$
s(i) = \frac{b(i) - a(i)}{\max{a(i), b(i)}}
$$

• $a(i)$：样本 $i$ 到同簇其他样本的平均距离（紧密性）

  $$
  a(i) = \frac{1}{|C_i| - 1} \sum_{j \in C_i, j \neq i} \text{dist}(i, j)
  $$

• $b(i)$：样本 $i$ 到最近其他簇所有样本的平均距离（分离性）

  $$
  b(i) = \min_{k \neq C_i} \left( \frac{1}{|C_k|} \sum_{j \in C_k} \text{dist}(i, j) \right)
  $$

• **$C_i$**：样本 $i$ 所属的簇

• $\text{dist}(i, j)$：样本 $i$ 和 $j$ 之间的距离（如欧氏距离）

取值范围	聚类效果
0.7~1	聚类结果清晰，结构强
0.5~0.7	结构存在但可能有重叠
<0.5	聚类效果差，样本归属不明确
接近-1	样本可能被分配到错误簇

肘部法则（Elbow Method）

1. 核心思想

通过观察簇内误差和（SSE）随聚类数K变化的拐点（”肘部”）确定最佳K值

2.计算

$$
SSE = \sum_{i=1}^{K} \sum_{x \in C_i} |x - \mu_i|^2
$$

• **$C_i$**：第 $i$ 个簇中的所有样本
• **$\mu_i$**：第 $i$ 个簇的质心（均值向量）

3. 结果解读

• 拐点对应的K值：通常为最佳聚类数

• 无明显拐点：数据可能无明确聚类结构

算法例子

线性模型

线性回归

1.最小二乘法基础原理

通过最小化残差平方和来估计参数，

• 残差：$e^{(i)} = h_\theta(x^{(i)}) - y^{(i)}$（预测值减真实值）

• 目标：找到参数 $\theta$ 使得 $\sum_{i=1}^m (e^{(i)})^2$ 最小。

  目标函数（均方误差）：

$J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$

其中：

• $h_\theta(x) = \theta^T x$（假设函数，线性预测）

• $m$：样本数量

• $\frac{1}{2}$ 是为了后续求导方便。

2.几何解释

寻找使所有数据点垂直距离平方和最小的超平面，

• 二维情况：拟合一条直线，使点到直线的竖直距离平方和最小。

• 高维情况：拟合一个超平面，最小化残差平方和

3.解析解推导

通过矩阵运算直接求解最优参数 $\theta$。

1. 矩阵表示：

   • 设计矩阵 $X \in \mathbb{R}^{m \times n}$（$m$ 个样本，$n$ 个特征）

   • 标签向量 $y \in \mathbb{R}^m$

   • 参数 $\theta \in \mathbb{R}^n$

2. 目标函数向量化：

   $$
   J(\theta) = \frac{1}{2m} | X\theta - y |^2
   $$

3. 对 θ 求导

   $$
   \nabla_\theta J(\theta) = \frac{1}{m} X^T (X\theta - y) = 0
   $$

4.正则化

为了解决过拟合或不可逆问题，引入正则化项。

• L1正则(Lasso)：$J(\theta) += \lambda||\theta||_1$

  • 产生稀疏解，可用于特征选择

• L2正则(Ridge)：$J(\theta) += \lambda||\theta||_2^2$

  • 防止过拟合，稳定数值解

特性	L1 (Lasso)	L2 (Ridge)
正则化项	$|\theta|_1$	$|\theta|_2^2$
解是否稀疏	是	否
特征选择	支持	不支持
处理共线性	部分有效	有效
计算复杂度	较高（需迭代优化）	较低（有解析解）

逻辑回归

Sigmoid

$$
g(z) = \frac{1}{1+e^{-z}}
$$

• 将线性输出映射到(0,1)区间

• 导数特性：$g’(z) = g(z)(1-g(z))$

交叉熵损失

$$
J(\theta) = -\frac{1}{m}\sum[y\log(h)+(1-y)\log(1-h)]
$$

• 对分类任务更敏感，梯度更新幅度与误差成正比

决策树模型

基础决策树

核心思想：通过递归的if-then规则划分特征空间，构建树形结构。

关键算法：

1. ID3（Iterative Dichotomiser 3）

   • 使用信息增益（Information Gain）选择特征

   • 仅支持离散特征，容易过拟合

2. C4.5（改进版）

   • 引入信息增益比处理特征取值多的偏差

   • 支持连续特征和缺失值处理

   • 通过剪枝（如悲观错误剪枝）降低过拟合

3. CART（Classification and Regression Trees）

   • 二叉树结构，支持回归（MSE）和分类（Gini指数）

   • 生成后剪枝（代价复杂度剪枝）

特点：

• 可解释性强，可视化直观

• 对异常值不敏感

• 容易过拟合（需通过max_depth/min_samples_leaf等参数控制）

随机森林（Random Forest）

核心思想：通过Bagging（Bootstrap Aggregating）集成多棵决策树，引入双重随机性降低方差。

关键技术：

1. 数据随机：每棵树训练时Bootstrap采样

2. 特征随机：节点分裂时从随机子集中选最优特征（√p或log2p）

3. 投票机制：分类取众数，回归取平均

优势：

• 天然抗过拟合（通过树间独立性）

• 可并行训练（scikit-learn默认n_jobs=1需手动设置）

• 提供特征重要性（基于Gini不纯度减少量或排列重要性）

变体：

• Extra-Trees（Extremely Randomized Trees）：进一步随机化分裂阈值

梯度提升树（GBDT/XGBoost）

1. GBDT（Gradient Boosting Decision Tree）

核心思想：通过加法模型（Additive Model）串行训练多棵弱树，沿负梯度方向迭代优化。

关键点：

• 损失函数：回归常用MSE，分类用对数损失

• 拟合残差：每棵树预测当前模型的负梯度（伪残差）

• 学习率（shrinkage）：控制每棵树贡献，防止过拟合

2. XGBoost（eXtreme Gradient Boosting）

核心改进：

• 二阶泰勒展开：损失函数使用一阶+二阶导数（类似牛顿法）

• 正则化项：在目标函数中加入叶子节点数（γ）和权重L2范数（λ）

• 工程优化：

  • 特征预排序（列块存储）

  • 加权分位数草图（Weighted Quantile Sketch）处理缺失值

  • 并行化设计（特征粒度并行）

特性	单棵决策树	随机森林	GBDT/XGBoost
训练方式	单次训练	Bagging并行	Boosting串行
过拟合风险	高	低	中等（需调参）
数据敏感性	对噪声敏感	鲁棒性强	需处理异常值
解释性	最好	特征重要性	全局重要性
典型超参数	max_depth	n_estimators	learning_rate

支持向量机（SVM）

名词解释

• 支持向量：离分界线最近的那些样本点，它们决定了分界线的位置。

• 间隔（Margin）：分界线到两侧最近点的距离，SVM的目标是最大化这个间隔。

线性可分（硬间隔）

找到一条直线w*x+b=0（超平面），使分类样本落在直线（平面）的一边，数学目标等同于最大化间隔。硬间隔要求严格可分。

线性不可分（软间隔）

如果数据存在噪声或重叠，允许一些样本点出错。数学目标引入最小化惩罚量。

线性不可分（核技巧）

数据无法用直线分开，SVM通过核函数将数据映射到高维空间使其线性可分。

聚类算法

聚类算法旨在将数据分类为若干簇，同一簇内样本相似，不同簇内样本相异。

K-means

核心思想

• 预先指定簇的数量（K），通过迭代优化将数据划分为K个球形簇。

• 中心点驱动：每个簇用一个中心点（质心）表示，数据点属于离它最近的质心对应的簇。

算法步骤

1. 初始化：随机选择K个点作为初始质心（如K=3）。

2. 分配数据点：计算每个点到所有质心的距离（通常用欧氏距离），将其分配到最近的质心所属的簇。

3. 更新质心：重新计算每个簇中所有点的均值，作为新质心。

4. 重复：直到质心不再显著变化（收敛）或达到最大迭代次数。

关键参数

• K值：通过肘部法（Elbow Method）或轮廓系数选择。

• 初始化方法：K-Means++（优化初始质心选择）。

• 最大迭代次数：防止无限循环。

优点	缺点
简单高效，适合大规模数据	必须预先指定K值（可能不准）
结果容易解释（球形簇）	对初始质心敏感（可能局部最优）
线性复杂度（计算快）	只能发现球形簇，对非凸簇失效
	对噪声和离群点敏感

DBSCAN

核心算法

• 基于密度：将高密度区域划分为簇，低密度区域视为噪声。

• 无需指定簇数量：通过数据分布自动发现任意形状的簇。

概念

• 核心点：在半径ε（epsilon）内有至少MinPts个邻居的点。

• 边界点：在ε内邻居数<MinPts，但属于某个核心点的邻居。

• 噪声点：既不是核心点也不是边界点。

算法步骤

1. 随机选点：选择一个未访问的点，检查其ε邻域内的邻居数。

2. 判断核心点：

   • 如果邻居数≥MinPts → 标记为核心点，新建一个簇，并扩展簇（递归检查邻居）。

   • 否则 → 暂时标记为噪声。

3. 扩展簇：将所有密度相连的核心点加入同一簇。

4. 重复：直到所有点被访问。

关键参数

• ε（epsilon）：邻域半径，影响簇的紧密程度。

• MinPts：核心点所需的最小邻居数，通常取3~5。

优点	缺点
无需指定簇数量	对参数ε和MinPts敏感
能发现任意形状的簇	高维数据效果差（维度灾难）
自动识别噪声点（抗噪能力强）	密度不均时效果不佳
适合不规则数据分布	计算复杂度较高（接近O(n²)）

降维方法

PCA（主成分分析）

核心思想

• 线性降维：通过正交变换，将原始特征转换为一系列线性无关的“主成分”。

• 保留最大方差：第一个主成分方向是数据方差最大的方向，第二个主成分与第一个正交且方差次大，依此类推。

关键步骤

1. 中心化数据：将每个特征减去其均值（使数据以原点为中心）。

2. 计算协方差矩阵：反映特征之间的相关性。

3. 特征值分解：找到协方差矩阵的特征值和特征向量。

4. 选择主成分：按特征值从大到小排序，取前k个特征向量作为新坐标轴。

5. 投影数据：将原始数据映射到选定的主成分上。

数学表示

• 第一主成分：

$$
PC1 = \mathbf{w}_1 \cdot \mathbf{X}
$$

其中，$\mathbf{w}_1$ 是最大特征值对应的特征向量。

• 降维后的数据

$$
\mathbf{X}_{\text{PCA}} = \mathbf{X} \cdot \mathbf{W}_k
$$

其中，$\mathbf{W}_k$ 是前 $k$ 个特征向量组成的矩阵。

应用场景

• 数据可视化（降到2D/3D）。

• 特征工程（去除冗余特征，加速模型训练）。

• 去噪（丢弃方差小的成分）。

优点	缺点
计算高效，适合大规模数据	只能捕捉线性关系
去除特征间的相关性	方差小的方向可能包含重要信息
可解释性强（主成分是线性组合）	对非线性结构失效

t-SNE（t-分布随机领域嵌入）

核心思想

• 非线性降维：专注于保留局部邻域结构，适合可视化复杂流形。

• 概率建模：在高维和低维空间中分别用高斯分布和t分布表示数据点的相似性，最小化两者差异。

关键步骤

1. 计算高维相似度：对每个点 ${x}_i $，计算与邻居 ${x}j $ 的相似度（高斯分布$p{j \mid i}$)

   $p_{j \mid i} = \frac{

   \exp\left(-\frac{\|\mathbf{x}_i - \mathbf{x}_j\|^2}{2\sigma_i^2}\right)
   

   }{

   \sum_{k \neq i} \exp\left(-\frac{\|\mathbf{x}_i - \mathbf{x}_k\|^2}{2\sigma_i^2}\right)
   

   }$

2. 对称化联合概率：通过对称化条件概率得到联合概率：

$$
p_{ij} = \frac{p_{j \mid i} + p_{i \mid j}}{2n}
$$

3. 低位映射：低维空间中的随机初始化点$y_i$使用 t 分布（自由度为1）计算相似度$q_{ij}$

$$
q_{ij} = \frac{
\left(1 + |\mathbf{y}_i - \mathbf{y}j|^2\right)^{-1}
}{
\sum{k \neq l} \left(1 + |\mathbf{y}_k - \mathbf{y}_l|^2\right)^{-1}
}
$$

4. 优化目标（最小化KL散度）

$$
\text{KL}(P | Q) = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}}
$$

特点

• 强调局部结构：邻近的点在低维中仍靠近，但全局距离可能失真。

• t分布的使用：避免“拥挤问题”（高维远距离点在低维被压缩）。

应用场景

• 高维数据可视化（如MNIST手写数字、基因数据）。

• 探索性数据分析（发现隐藏的簇结构）。

优点	缺点
能揭示非线性结构（如簇、流形）	计算复杂度高（O(n²)）
可视化效果极佳	结果受超参数影响大（困惑度Perplexity）
适合高维数据探索	不能用于特征工程（每次结果不稳定）